1283. Банковская реформа
По непроверенным
слухам надвигается банковская реформа, и Вы решили внести в неё свои
предложения – а вдруг да примут, да ещё может и за идею что-нибудь заплатят?!
Ваша идея
состоит в том, чтобы в обращении изменить номиналы разменных монет. По Вашему
мнению, это должны быть монеты достоинством 1, 5, 10, 25 и 50, а как будут
называться мелкие деньги - пусть решает Центральный Банк.
Однако
Центральный Банк тут же потребовал от Вас предоставить сведения, о том,
сколькими способами можно предоставить ту или иную сумму в мелких деньгах до
7489 включительно. Почему до этой суммы? И как банк их назовёт? Да кто его
знает: у банкиров свои причуды, мы же назовем их для простоты просто монетами.
Например, сумму
в 11 единиц можно предоставить в виде: 10 * 1 монета + 1 * 1 монета, или 5 * 2
монеты + 1 * 1 монета, или 5 * 1 монета + 1 * 6 монет или 11 * 1 монета, то
есть всего четырьмя способами.
Ваша задача
написать программу, считающая указанное количество способов, чтобы Вы могли
быстро отвечать на любые запросы банкиров.
Вход. Каждая строка
содержит по одному натуральному числу – очередной банковский запрос.
Выход. Для каждой
строки ввода вывести в отдельной строке искомое количество способов
предоставления заданной суммы.
|
Пример входа |
Пример выхода |
|
11 5 26 |
4 2 13 |
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Обозначим через
f(k, n) количество способов составить сумму n из первых k
номиналов монет. Оно равно количеству способов составить сумму n первыми
(k – 1) номиналами (то есть без использования k-го номинала) плюс
количество способов составить сумму (n – ak) при
помощи k номиналов. Имеем соотношение:
f(k,
n) = f(k – 1, n) + f(k, n
– ak)
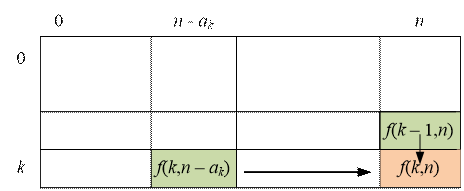
Изначально
положим f(0, 0) = 1, f(0, n) = 0, n > 0.
Пример
Сумму s = 11 можно выдать 4 способами:
1)
10 + 1
2)
5 + 5 + 1
3)
5 + 1 + 1 + 1 + 1 + 1 + 1
4)
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 +
1
|
|
k \ n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
начало |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
c = 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
c = 5 |
2 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
|
c = 10 |
3 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
4 |
4 |
Номиналы
в 25 и 50 центов не повлияют на результат для суммы в 11 центов.
Рассмотрим
например равенство f(2, 10) = f(1, 10) + f(2, 5). Оно означает,
что количество разбиений числа 10 при помощи двух номиналов монет 1 и 5
включает в себя:
·
f(1, 10) = 1, количество
разбиений числа 10 одним номиналом 1 (разбиение 10 = 1 + 1 + 1 + … + 1).
·
f(2, 5) = 2, количество
разбиений числа 5 двумя номиналами 1 и 5 (разбиения 5 = 1 + 1 + 1 + 1 + 1 и 5 = 5).
Реализация алгоритма
Объявим глобальные массивы.
#define MAX 7500
long long mas[MAX];
int
coins[11] = {1,5,10,25,50};
Основная часть программы.
memset(mas,0,sizeof(mas)); mas[0] = 1;
for(i
= 0; i < 5; i++)
{
for(j =
coins[i]; j < MAX; j++)
mas[j] += mas[j - coins[i]];
}
Читаем входные данные и выводим
результат.
while(scanf("%d",&n) == 1)
printf("%d\n",mas[n]);
Реализация алгоритма – рекурсия с запоминанием
#include <stdio.h>
#include <string.h>
int i, j, n;
int dp[6][7500];
int a[6] = { 0,1,5,10,25,50 };
int f(int k, int n)
{
if (k == 0
&& n == 0) return 1;
if (k == 0 || n
< 0) return 0;
if (dp[k][n] !=
-1) return dp[k][n];
return dp[k][n] = f(k
- 1, n) + f(k, n - a[k]);
}
int main(void)
{
memset(dp, -1, sizeof(dp));
while (scanf("%d", &n) == 1)
printf("%d\n", f(5, n));
return 0;
}
Java реализация
import java.util.*;
public class Main
{
static int dp[][] = new int[6][7500];
static int a[] = {0,1,5,10,25,50};
static int f(int k, int n)
{
if (k == 0
&& n == 0) return 1;
if (k == 0 || n < 0) return 0;
if (dp[k][n] != -1) return dp[k][n];
return dp[k][n] = f(k - 1, n) + f(k, n - a[k]);
}
public static void
main(String []args)
{
Scanner con = new Scanner(System.in);
for(int i = 0; i < 6; i++)
for(int j = 0; j < 7500; j++)
dp[i][j] = -1;
while(con.hasNext())
{
int n = con.nextInt();
System.out.println(f(5,n));
}
con.close();
}
}